Les calculs kantikes
Au hasard des défis, celui d'expliquer le kantike est tentant.
Quel calcul? Et comment kil est puissant ?
QBIT
On partira donc d'un "qbit", nom affolant évoquant l'intrication je vous dis pas.
Son état final est 0 ou 1 comme de juste, mais il se calcule pas comme ça: il est en fait dans un état
qb = a*Zéro + b *Un = (a,b) avec bien sur a^2 + b^2 = 1. Ce sont des probabilités.
En fait un qbit qui n'est pas DEJA Zéro ou Un, va évoluer comme un grand vers l'un ou l'autre, (Zéro ou UN) avec la probabilité a^2 ou b^2. Bien sur les deux probabilités sont liées (leur somme fait un).
Un point important, généralement passé sous silence et pour cause, il est troublant et se trouve être l'essence véritable du quantique, sa caractéristique première, son absolue bizarrerie: les coefficients "a" et "b" sont (bien sur) des nombres complexes...
Le qbit n'est donc pas un cercle mais une sphère, la sphère dite de "Bloch", l'oscillation entre les deux états opposés, les deux pôles de la sphère (1 et 0), se faisant en passant par les points de la surface de la sphère.
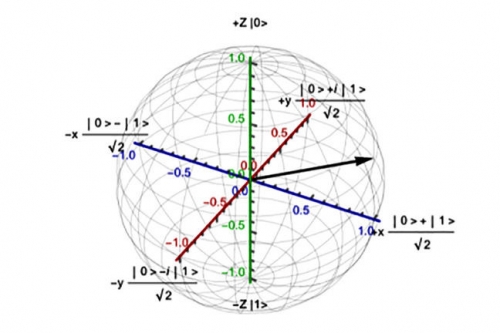
Heureusement, le complexe peut ne pas être imaginaire (toujours), et le coefficient se réduire à un nombre ordinaire: cela devrait suffire à notre intuition bornée, ouf. Mais tout de même...
Calculer
Le calcul kantike consiste donc à:
- préparer des qbits, comme des couples (a,b)
- leur appliquer des transformations variées qui les transforment en (a',b')
- mesurer a' (et/ou b') en regardant les qbits se transformer.
Les transformations
1) Par exemple, on sait faire des transformations sur un qbit comme le "NOT" qui comme de juste, échange le Un et le Zéro:
NOT (a,b) = (b,a)
2) On sait faire aussi une opération trés "transistor", le "non contrôlé" (en fait il s'agit d'une négation contrôlée, au contraire), qui ne fait le non que quand il faut (un vrai rêve). On a donc un Qbit de contrôle et un Qbit de valeur.
On les accouple et hop ils se transforment ! En fait dans le résultat, la valeur du deuxième va dépendre de celle du premier. En gros, si le premier vaut zéro, on reste comme on est, sinon on s'inverse.
cNOT (0 0/1) = (0, 0/1) : pas de changement
cNOT (1, 0/1) = (1, 1/0) : on inverse.
3) On sait aussi faire le Hadamard, dit H (grand hache), et qui fait:
(On note V2 racine de 2)
H 1 0 = 1 1 /V2
H 0 1 = 1 -1 /V2
Comme le kantike c'est linéaire, on remarque que H o H est l'identité:
H a b = (a a) + (b -b) = (a+b) (a-b) / V2
H H a b = 2a 2b / V2 / V2 = a b
H se représente bien sur par une matrice:
1 1
1 -1
4) Il y en a plein d'autres...
Notons que ces "calculs" sont réversibles, c'est à dire que comme il ne peuvent être réalisés que par des opérations physiques par définition réversibles, et bien ils ne peuvent pas être destructifs... Pas moyen de mettre un Qbit à zéro complètement.
On montre qu'on peut quand même faire de l'algorithmique réversible, par ailleurs.
Plusieurs Qbits
Quand on couple les qbits, on obtient des intrications. C'est là qu'on peut exprimer le miracle de la transmission de pensée à distance.
Soit le bi-qbit (2 qbits) ( 00 + 11 ) /V2
Alors qu'en toute rigueur un biqbit doit avoir 4 coefficients (2 ^N avec N nombre de qbits) ici on en a pris un un peu spécial. Bon disons que si les deux qbits sont séparés par disons de chez moi à chez vous, et qu'on réduit le système et qu'en plus on obtient zéro, et bien, hop, vous vous aurez zéro. Pareil pour le un. C'est ça la magie du kantike.
J'avoue que cette explication, formelle et matheuse m'enchante complètement. J'ai -vraiment- l'impression d'avoir compris l'intrication. Cet état est l'état dit "de Bell".
Bien sur les opérations Hadamard et cNOT opèrent sur des états intriqués. On a là l'essence du calcul kantike: plongés dans l'hyperespace de l'intrication, couplage absolu ensorcelant, on peut hacker et là ça va dépoter.
Memoire
Y a mieux: un état quantique c'est donc 2^N coefficients complexes pour un système à N qb. Ces coefficients sont "stockés" dans le système qui a donc une capacité mémoire en regard. Le système Sycamore de Google, à 53 qb, a donc une mémoire (un double float fait 8 octets) 8*2^53 = 64 * 10^15 = 64 peta octets.
Le parallélisme
Le caractère parallèle du calcul kantike est difficile à appréhender, mais pas tant que ça. Disons que quand on a N Qbits, on a un état qui se décrit par 2^N vecteurs propres. L'application d'une fonction sur cet état intriqué se trouve en fait utiliser 2^N coefficients qui sont donc opérés en parallèle. Voilà l'accélération. Imaginons 100 Qbits: le degré de parallélisme est exponentiellement supérieur au classique et voilà toute l'histoire...
Suprématie
La suprématie quantique, annoncée brièvement en Septembre 2019 sur une page soudainement retirée de la vision publique est évidemment une plaisanterie(3). Mais les gens y travaillent.
Le chiffre de 53 Qbits stabilisés est vu comme une limite à franchir (5), et il semble que le premier avion toilé maladroitement et volant comme une chauve souris ivre, ait décollé.
(1) https://www.intriq.org/uploads/Documents/Activités/Cegep2016/Alexandre%20Blais.pdf
(2) http://dept-info.labri.fr/~ges/ENSEIGNEMENT/CALCULQ/polycop_calculq.pdf
(3) https://www.scottaaronson.com/blog/?p=4317