Les fonctions (Quatre)
Au hasard du web, on peut trouver de la vraie, de la bonne pédagogie. On a vu (1) et on en est très content.
D'abord pas de flatMap, un "bind" qui compose, non pas deux bêtes fonctions, mais, et c'est là toute la question, deux embranchements de cette sorte:
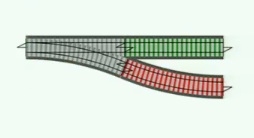
On a ici en fait une fonction avec un "traitement d'erreur". Pour les composer, on va faire:

J'adore cette représentation, qui illustre très bien comment le flatMap ou "bind monadique" rassemble tous les flots d'erreurs et permet de composer en fait simplement les blocs de lego...
Que cela fasse de la composition monadique une sorte de monoïdisation de la composition de programmes porteurs d'effets, et donc, que si ces effets sont de même type donc "endo", on aie des monoïdes dans la catégorie des endofoncteurs, et bien cela est tout à fait naturel et évidemment compréhensible.
Bravo à l'orateur !
Le monoïde
Au passage, il fait très bien comprendre ce qu'est le fameux "monoïde", abstraction ultime ou première abstraction, c'est selon. On a fait exprès ici de ne pas commencer par ça.
En gros, c'est un truc qu'on peut additionner. A partir de là, on en abstrait la sommation indéfinie, qui permet alors au concept de transcender l'infini. Et oui.
Anéfé, toute addition de PLUSIEURS instances d'un monoïde se confronte à la répétition, et donc à l'accumulation indéfinie d'une même chose (une addition). D'où la nécessité de la contrôler programmatiquement:
--------
totalisateur = 0
for(pour) chaque "i" dans l'intervalle 0..N , N exclu, faire la chose suivante:
additionne totalisateur et l'élément i et remplace totalisateur par le résultat
---------
Ce contrôle répétitif, esclavagiste, est l'archétype de l'horreur impérative non abstraite.
On a ici la projection, ou plutôt l'incessante répétition rituelle de l'horreur du for, dont l'abstraction se nomme "fold":
(fold 0 add) est la -fonction- qui somme TOUS les éléments monoïdaux d'une séquence indéfinie de ceux ci, en partant de zéro.
Elle est la sommation monoïdale: un objet calculatoiresque, un animal vivant, un esprit à invoquer pour faire le boulot, une arme libératrice.
Dans les exposés pédagogiques courants, on se focalise sur la programmation en style fonctionnel de la chose. Cela est bien sur une erreur totale: la vraie compréhension de la chose est que l'implémentation véritable EST la boucle for impérative, parangon de ce que font les pauvres programmeurs impérativés toute la journée...
La révélation doit être immédiate: FP for ever...
Et puis on peut avancer encore.
En effet, les fameuses "lois" du monoïdes que l'on s'empresse d'asséner stupidement n'ont évidemment aucun intérêt "en soi". Elles ne sont que des propriétés additionnelles qui peuvent être utilisées ou pas.
Par exemple, le cas donné par notre brillant pédagogue des logs de la journée dont on veut la synthèse hebdomadaire. Faut il vraiment tout additionner tous les jours pour synthétiser le week end un monstre multi gigabité ?
Alors qu'"évidemment", on peut synthétiser tous les jours et du fait d'une propriété intéressante, l'associativité de cette addition là, n'additionner une fois par semaine QUE les synthèses, de bien plus petites tailles.
Au passage, on comprend avec ce cas là, EN PLUS, le véritable intérêt de cette histoire de monoïde, et mieux comment s'en servir utilement. On a ici deux types de monoïdes dont on peut sommer les éléments associativement. En projetant l'un sur l'autre, c'est ça l'idée, mettre en correspondance avec le bon monoïde; on optimise...
SOLID
On se doit d'évoquer les grands principes de l'orienté objet, dont se gargarisent les pédants pour mieux nous enfumer...
Le mot est SOLID, formé des lettres des initiales de "bons" principes.
- S(olid) ingle responsability: "only one reason to change" or "do only one thing well".
Evidemment une fonction peut faire ça
- sol(I)d nterface segregation: "one interface per function" or "one function per interface".
A function is an interface, isnt'it ?
- s(O)lid : pen Closed principle: "only change a class to fix a bug". Open to extension Closed for change.
Bien sur, cela suppose l'héritage. En fait non.
- so(L)id : Liskov "substitution principle" : "dont change what your parent dont". "be a good son"
En fait la contravariance appliquées à des fonctions ferait la chose...
- solid(D): Dependency Inversion. The holywood principle: dont call us, we call you.
Les patterns fonctionnels
Le pédagogue présente aussi la célèbre mise en correspondance des fameux patterns orientés objets et des patterns fonctionnels équivalents: la partie droite n'est composée que des mots "fonction", tous les patterns OO n'étant que des resucées variées de la bonne idée qui consiste à considérer un programme (une fonction) comme une donnée, parangon depuis toujours de l'idée qui est la bonne et qui fut occultée cinquante ans.
L'imam caché est là. Ca va être la fin du monde.
Les renversements de tendance
Au sujet de la fin du monde, maintenant passée (...), il convient de faire remarquer, que comme on l'a vu, appliquer le pattern "interpreter" pour calculer à run-time un programme qu'on va exécuter à la fin revient à faire deux choses opposées: se mettre à la place du compilateur pour construire un programme à sa place, et aussi s'en affranchir pour manipuler les structures calculatoires qu'il se charge d'optimiser ordinairement... Comme les temps changent.
Et puis bien sur il y a l'inversion de pratique qui mène de l'idée d'objet (association entre la donnée et le comportement) et son inverse strict (la séparation absolue des données et des fonctions). Ces passages à 90 degrés qui ponctuent le passage du temps sont fascinants.
(1) la très pédagogique présentation: https://vimeo.com/113588389
(2) Une sorte de somme http://gorodinski.com/blog/2013/09/18/oop-patterns-from-a-functional-perspective/