Le théorème de Pythagore
Au fait comment on le démontre ?
La démonstration d'Euclide est tout de même contournée:
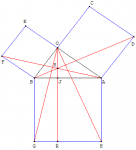
Elle est entièrement basée sur un lemme: deux triangles inscrits dans un rectangle avec un coté commun ont même surface, égale à la moitié de celle du rectangle.
Le carré de gauche a pour surface a carré, celui de droite b carré et celui du bas c carré.
Le triangle BFA est le triangle BOG tourné de 90 degré vers la gauche.
Sa surface est la moitié de celle du carré de gauche.
De la même manière le triangle BOG a pour surface la moitié du rectangle BJKG qui a donc pour surface a au carré.
Un raisonnement similaire nous donne b au carré pour le rectangle JAEK.
et donc, c carré égale a carré plus b carré.
La démonstration de Léonard de Vinci est bien plus belle:
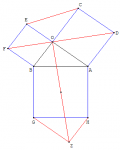
On déplace juste les structures...
On fera un déplacement de O sur F et de B sur E...
Il devient alors évident que les deux hexagones du haut et du bas sont égaux et en retirant les deux triangles d'origine, on a égalité entre le carré du bas et les deux carrés de droite et de gauche.
Les deux hexagones sont bien sur FEGDAB et OAHIGB
Y a celle de Bonaparte, qui tourne à l'évidence brute:
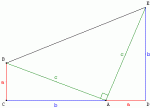
On duplique le rectangle à problème.
La surface du trapèze c'est bien sur la moitié de (a+b) au carré.
Donc le triangle du milieu a pour surface celle du trapèze moins deux fois la surface du triangle rectangle:
(a+b) carré - 2 (a*b) = c carré = a carré + b carré