Les qubits

On avait évoqué avec "les équations" (1) la notion d'espace de Hilbert, chaque coefficient de l'espace vectoriel étant complexe, ce qui justifie le qualificatif de "Hilbertien" attribué à cet espace... 

On passera donc directement à l'espace de représentation qu'est un qubit, défini  un espace de Hilbert à DEUX dimensions, et certainement pas comme un "vecteur", élement de l'espace. DEUX nombres complexes définissent donc l'état d'un qbit. On notera donc bien que pour supporter le calcul, on ne satisfait pas d'un seul axe, même modulé façon complexe: le qubit déploie sa binarité sur DEUX axes, dans DEUX dimensions. 

On a suivi les vidéos anciennes mais didactiques (2) et on les résumera ici... 

qubit

Tout d'abord le qubit a un "u", et "qu" (prononcez "cul") est incontournable. C'est un espace de vecteurs, et chaque vecteur est un "ket", en fait une combinaison linéaire de kets de base, à coefficients complexes (on ne le dira jamais assez). 

v = alpha |0> + beta |1> 

|0> est le ket "0", premier vecteur de la base vectorielle choisie ici. À condition que ce vecteur-là soit effectivement l'un des axes choisis par un système de mesure choisi, par exemple, une direction de spin déterminée, ou un axe de polarisation donné, et bien après une mesure, le vecteur est détruit et le résultat sera l'un des deux axes, avec une probabilité de alpha * alpha^ (si on note ^ la barre verticale de la conjugaison complexe) (béta respectivement, bien sur). 

Un vecteur est normé, donc alpha*alpha^+ beta*beta^ = 1.

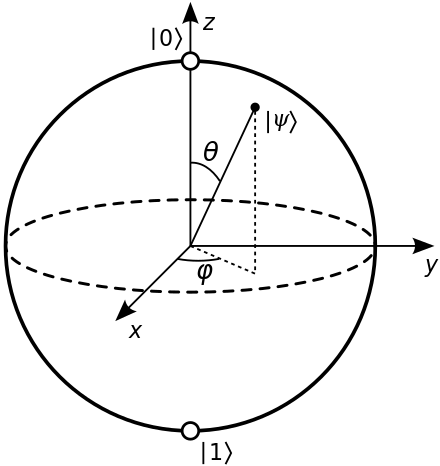
On peut ainsi représenter un état de qubit comme un point sur une sphère, le déplacement sur la sphère étant dû au caractère complexe des coefficients. Si les complexes ont la même "phase", ils feront de leurs points représentants les esclaves d'un méridien... Le qubit est donc une  boule et voilà. Notons qu'il n'y a bien que DEUX vecteurs de base, et qu'en fait, tout se passe comme si il y avait DEUX cercles d'évolution des vecteurs , le deuxième étant rabattu de 90° pour faire l'équateur... Bref la bouboule est virtuelle mais on voit très bien ce que je veux dire ou pas. Notons en fait que la sphère de Bloch est constituée des deux vecteurs 0> et 1> en opposition. 

 

Pour faire des espaces de qubits plus complexes, on fait des produits dit "tensoriels" qui consistent à multiplier les coefficients de manière combinatoires pour définir des objets (vecteurs) dans des espaces à 2^(nombre de qubits) dimensions. 

Le vecteur (a0, a1) combiné (par le produit tensoriel) au vecteur (b0,b1) donne l'ensemble de deux qbits intriqués (a0*b0, a1*b0, a0*b1, a0*b1) dans un espace de dimension 4. On notera comment se fait l'intrication: le vecteur (a0, a1) d'abord multiplié par b0 , puis par b1... 

Pour avoir l'esprit bien clair, on dira que |0> = 1* |0> + 0*|1> , soit le vecteur (1, 0), et que |1> est le vecteur (0,1). 

 On passera ensuite aux portes sur un seul qbit, définies par des matrices 2x2 unitaires. 

Note: "unitaire" signifie pour une matrice M que (conjuguée de la transposée de M) * M = ID. Cela permet de conserver le caractère normé des vecteurs qu'on transforme. 

Porte

Une porte sur UN qubit est donc une matrice unitaire à 4 coefficients complexes (bien sur). 

La porte NOT sur un qubit est la matrice (0 1)(1 0) qui échange les coordonnées. NOT NOT = ID bien sûr. 

La notation matricielle adoptée consiste à exprimer les colonnes de la matrice horizontalement, et en succession... 

La porte Controle NOT, sur DEUX qubits, applique le NOT sous contrôle. Sa matrice est : 

1 0 0 0 ,  0 1 0 0,  0 0 0 1  ,  0 0 1 0 

Cela se visualise par: 

------------

     |

----O------

Entre deux lignes de qbits... 

cNOT s'exprime aussi en faisant des produits tensoriels de vecteurs: | x , y > sera transformé en |x, y + x>, avec '+' l'addition modulo 2... 

On terminera l'exposé par l'essentiel: TOUS les programmes quantiques se matérialisent par des lignes parallèles de qbits, décorées par : 

- des portes sur UN qubit

- des cNOT entre deux qubits

 

Etpicétout. Assez simple, en fait. 

 

4 portes

Mentionnons les 4 portes mono qubit essentielles. On donne les matrices, données par leur vecteurs colonnes listés horizontalement, et aussi par leurs actions sur les deux kets de base, 0> et 1>. 

I = (1 0)(0 1)    x> . I = x>

X = (0 1) (1 0)   0>.X == 1>, 1>.X == 0> 

Y = (0 i) (i 0)         0>.Y ==  i.1 > ,      1>.Y ==  i.0

Z = (1 0) (0 -1)     0>.Z == 0>   ,   1>.Z == -1

et voilà. 

On doit lui ajouter la porte d'Hadamard, dont la matrice est (1/V2)* (1 1) (1 -1) ,  0> .H == 0> + 1> , 1>.H == 0> - 1>

Bell 

Il faut mentionner alors les groupes de 2 qubits, base de tout. On fait donc les produits tensoriels des deux espaces de Hilbert que constituent chacun des qubits. (1/V2 ) * 00> sera donc un vecteur normé de cet espace de dimension 4...

 

D'abord les états de Bell ( non pas Alexander Graham, mais John Steward). 

Ils sont notés comme des combinaisons à partir de l'état de Bell archétype de l'état "intriqué" (intangled). 

1/V2 * ( 00> + 11> ) 

Vecteur dont on voit qu'il a des coordonnées dans les DEUX qubits (espaces associés). L'intrication vient de là. Les deux espaces ne sont pas séparés mais fusionnés. Comme la fusion intervient en dimension 4, on n'a pas d'intuition géométrique de ce qui se passe vraiment... 

L'état de Bell vient de la séquence de deux opérateurs: H I  (Hadamard sur une ligne, Identité sur l'autre), suivi de cNOT, le tout appliqué à l'état 00>. On a donc un moyen simple de fabriquer un état intriqué à partir d'un état "normal" obtenu par simple juxtaposition de deux états élémentaires... 

 On a en effet, 00> .HI = 0+1, 0> = 0,0> + 1,0> transformé par cNOT en   00> + 11>, qui est l'état de Bell. 

Les 3 autres états sont: 

1/V2 * ( 00> - 11> ) 

1/V2 * ( 01> + 10> ) 

1/V2 * ( 01> - 10> ) 

Ils forment une base de l'espace des 2 qubits, et sont tous les états (vecteurs) les "mieux" intriqués. 

Chacun de ces états corrèle deux probabilités de mesure et exprime la "communication instantanée" de Bell qui en viole les inégalités. Une pure merveille de théorie en pratique, au service du calcul. 

(1) http://francoiscarmignola.hautetfort.com/archive/2021/07/04/les-equations-6325261.html

(2) https://www.youtube.com/watch?v=F2okky5vD8k&list=PL1826E60FD05B44E4&index=10