Les bayésiens

La question de la probabilité a deux grandes interprétations, dont la première, celle basée sur l'émergence d'une ratio hors d'un grand nombre de cas dont les fréquences relatives finissent sous l'effet du nombre par devenir absolues et suivent des règles intangibles promues au rang de lois, domine et fait l'examen des expériences scientifiques.

La seconde, est elle basée sur l'incertitude chiffrée d'un examinateur subjectif regardant quelques cas qui confirment sans preuves véritables l'incertain... Les bayésiens sont des lascars obstinés et continuent de fasciner, voire d'opérer et cela partout. 

On en vient au probabilités qui font l'objet de formalisations mathématiques variées, mais on ne peut se départir de chercher des formes intuitives à ce qui continue de fasciner pour des raisons évidentes: la prédiction de l'avenir reste l'incontournable forme du coté attirant du savoir: comment ? Vous sauriez le futur ? Et oui, car je connais le passé et ses lois...

Pour commencer et pour mettre les choses au clair, la polémique entre bayésiens et fréquentistes a ainsi DEUX aspects qui n'ont rien à voir en apparence, alors que. 

Le premier est la divergence sur l'interprétation de la notion même de probabilité: mesure de la confiance ou limite d'une fréquence de mesure répétée ?

Le second est la la divergence sur la manière dont on calcule, les bayésiens partant d'une situation "a priori" que les fréquentistes contestent, cette situation à priori étant justifiée par l'interprétation bayésienne de la probabilité...

Le Sida

Connaissant le caractère mental du sida, on explorera le cas de base, celui du test d'hypothèse, en partant d'une prévalence du Sida de 1% dans population et d'un test rapide efficace à 99% dans ses deux caractères de "sensibilité" (pourcentage des sujets infectés dont le test est positif) et de "spécificité" (pourcentage de sujets non infectées dont le test est négatif). 

On remarquera l'utilisation du mot "sujet", alors qu'il s'agit bien sur d'objets, personnes innocentes à laisser tranquille ou à plaindre d'une mort atroce.

A partir de là on affirmera que si la prévalence du mal est (dix moins "q"= 10^-q)  et la précision du test (1 - dix moins "s" = 1 - 10^-s) , et bien la probabilité d'être atteint quand le test est positif sera :

1  / 1 + 10^(q - s)  

ce qui fait  exactement 1/2 dans le cas explicité ici où q = s = 2. 

 

La démonstration

On utilisera un arbre de manière à établir le plus vite possible les 4 probabilités des 4 cas. 2 modalités (oui/non on a le sida ou non, et ok/nok, le test est positif ou non). Cela doit être calculé en fonction des données données, et interprété suivant le sens des mots.

Par exemple ici oui = 10^-q,  quand q=2, 1%. 

Le point important, en fait fondamental, dans les probabilités croisées, est d'établir les grandes régions aggrégantes par exemple la région "oui", divisée par les régions "ok" et "nok", la question posée étant celle de la probabilité dite conditionnelle suivante: "oui sachant ok", c'est à dire la division par la probabilité de ok de la probabilité d'être à la fois oui et ok. Les grandes régions sont ainsi bien sur oui, ok , non et nok elles-mêmes interpénétrées mutuellement. 

On en vient à la première définition "bayésienne": la probabilité de "A sachant B" est : P(A/B) = P (A^B) : P(B) 

qui définit la probabilité dite conditionnelle, le symbole de la division étant : et le "^" exprimant bien sur l'intersection, ou le "à la fois", qui bien sur n'est en aucun cas une multiplication des probabilités correspondantes. 

On en déduit d'ailleurs immédiatement le fameux théorème qui n'en est pas un, d'ailleurs, étant immédiatement issu de la définition de la probabilité conditionnelle. La probabilité de A^B ("A inter B") étant évidemment égale à

P(A/B)*P(B) et à P(B/A)*P(A) par conséquent égaux eux-mêmes et donc: 

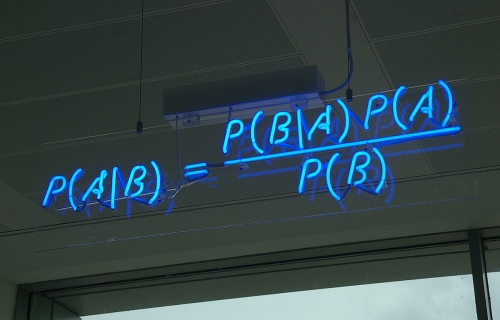
On passera donc immédiatement sur cette histoire de "théorème" parfaitement fétichisée et sans aucun intérêt d'ailleurs, sinon le fait qu'il affirme simultanément deux fois un bête définition pour une expression linguistique elle dotée de sens, le fameux "a sachant b" qui apparait fréquemment dans les questions et les réponses des vrais problèmes. On a donc un contresens (un théorème qui n'en est pas un) pour une signification profonde (on exprime des vérités dotées de sens à travers des formes calculatoires non totalement triviales). 

On ajoutera aussi aux "trucs" de Bayes la "décomposition" ultra utile et également directement issue de la définition de la conditionnalité:  p(X) = P(X/A) . P(A) + P(X/B) . P(B)  

Ainsi, pour répondre à la question fondamentale et terrible "ai-je le sida quand je suis positif ? ", on doit calculer une probabilité conditionnelle en en connaissant deux. 

La première, la question angoissée est "oui sachant ok".

Les deux données sont ce qui caractérise le test : la sensibilité,  soit "ok sachant oui" , et la spécificité "nok sachant non". On les supposera égales. Soit S= 10^-s égal à 1 - Q = 10^-q

ok/oui = nok/non = 1 - S = 1 - ok/non , ok/non  = S

On en vient alors à la question posée. 

oui/ok = ok/oui . oui : ok 

Or,  ok = ok/oui.oui + ok/non.non , comme on l'a vu, c'est ce que j'ai appelé la "décomposition de Bayes". 

Donc: 

1 : oui/ok = 1 + non . ok/non : oui . ok/oui

=  1 +   S (1- Q) / (1 - S) Q  

= 1 + 10^q-s   (1 - 10^-q)/ 1 - 10^-s)  

Ce qu'il fallait démontrer, le facteur correctif valant 1 en gros dans la plupart des cas. 

Si s = 2 et q 4  (prévalance de 1 pour 10 000, soit 0,01%) 

resultat = 1 : (1 + 10^4-2 (.9999/.99))  = 1 : 101 * (1.01) = 0,01% 

Plus la prévalence est faible, disons inférieure à la sensibilité du test, moins le résultat est inquiétant... En fait et c'est la grande leçon, il faut pour que le test prévoie plus qu'une possibilité non nulle, que sa sensibilité soit supérieure à la prévalence...

Ainsi un test sensible positif peut ne PAS entrainer d'inférence statistique en faveur de l'hypothèse qu'il teste. Cette erreur est l'"erreur du taux de base négligé". 

L'interprétation bayesienne 

On peut présenter la chose autrement. 

oui/ok = oui * X 

C'est à dire que si on part de "oui" la probabilité d'avoir le SIDA "en général", (on dit la probabilité "antérieure") on va chercher, sachant X, un facteur multiplicateur de risque (ou ratio de vraisemblance) à obtenir la probabilité "améliorée" par l'expérience d'avoir le SIDA, soit la probabilité "postérieure".

Le facteur multiplicateur est bien sur: X = ok/oui : ok   qui, et c'est ça l'essentiel, NE DEPEND PAS de la prévalence...

ok se calcule par décomposition:

ok = oui * ( ok/oui)  + (1 - oui) * (1 - nok/non)

1-oui == 1 (oui est très faible) 

ok == 1 - nok/non   

Donc, on a X = sensibilité/ (1 - spéficité) soit environ 10 ... 

Ce ration est extrêmement important, et montre que pour les prévalence de moins de 10%, l'augmentation du risque mesurée par le test, tout important qu'il soit ne donne pas de probabilité sensible d'avoir le SIDA.

Par contret, et là Bayes montre qu'on peut améliorer une connaissance, SI la personne est (du fait de ses mauvaises fréquentations) dans une population dont le risque est de 10%, et bien le test est intéressant à faire et peut se trouver décisif.  

L'autre démonstration 

On peut faire de tout ça d'autres démonstrations. 

Prenons le diagramme de Venn et ses 4 régions: périphérique (n), et (p), (pc), (c)

p pour "positif non contaminé", c pour "contaminé non positif" , n pour "non positif, non contaminé", pc pour "positif ET contaminé.

On a donc: 

(1)  1 = p + c + pc + n 

(2)  fop = p  / (n + p)   les faux positifs sont la proportion de positifs non contaminés parmi les non contaminés disont 1%

(3) vrp = pc / ( c + pc ) les vrais positifs sont la proportion de positifs contaminés parmi les contaminés disont 90% 

(4) c + pc = 10-5    les contaminés sont peu nombreux dans la population globale. 

A partir de là , on cherche la proportion de contaminés parmi les positifs:  x = pc  / (pc + p)  

(1 & 4)  p + n = 1 , une approximation évidente

(1 & 5) fop = p 

(3 & 4) pc = vrp . 10-5 =   9 . 10-6

x = 9.10-6 / (  9.10-6 + 10-2) = 9.10-4 = 10-3 

Plus exactement, si v  est la prévalence, soit c + pc, la proportion de contaminés. 

vrp = pc / v   et donc pc = v.vrp  

x = v.vrp ( v.vrp + fop) 

Or vrp vaut 1 en gros (la plupart des contaminés sont positifs) donc x  = v / (v + fop) = 1 / (1 + fop/v)

On doit donc comparer les faux positifs à la prévalence et c'est toute la question. x = v/ fop 

 

 

Q de Yule

Au fait si on examine les 4 cas possibles, sujet atteint (V ou F) et test positif ou non (P ou N), A, B, C, D avec 

A=PV, B=PF, C=NV, D=NF, le coefficient Q de Yule va désigner l'efficacité du test  Q = AD-BC/AD+BC

Le bayésianisme

C'est alors qu'on en vient à l'interprétation. Que signifie ces chiffres, se disant être des "probabilités" ? Des probabilités de "quoi" ? On a deux théories. 

La première est qu'il s'agit de la probabilité d'un événement considéré comme une mesure de sa fréquence d'apparition, la seconde est qu'il s'agit d'une mesure de la croyance en sa réalisation.

La chose n'existe pas, elle n'est qu'une possible apparition, mesurée par son existence parmi une multiplicité d'autres, ou bien par un degré de croyance, subjectif mais quantifié, en son apparition.      

L'attitude

Mais avant de gloser davantage, il convient de revenir aux fondamentaux. On se positionnera ici comme un statisticien expérimentateur dont on doit de décrire la posture et l'attitude  "typique".

D'abord il y a une réalité qu'il mesure, et qui se comporte conformément à un modèle statistique. On fait un test, et la question est: est qu'il s'est passé quelque chose qui dévie du modèle statistique ? 

L'hypothèse de base  est que non, il ne va rien se passer: l'hypothèse dite "nulle" sera  vérifiée: le monde est bien conforme au modèle évoqué et le test lui appartient. A moins que, et là on discute. Dans certaines circonstances, il va falloir décider de rejeter l'hypothèse nulle et d'adopter l'hypothèse alternative. Dans lesquelles ? 

Le test se traduit par une distribution de probabilité, disons par un pic, qu'on va positionner par rapport au modèle connu. Pour cela, on va calculer une valeur dite "p-value" ou "valeur p" qui va être la probabilité pour que dans le modèle connu, on soit encore éloigné encore plus de la moyenne connue que la mesure. Si l'hypothèse zéro est représentée par une densité de probabilité, on va l'intégrer au delà de la valeur moyenne de la mesure test.

Cette probabilité va alors être comparée à un seuil, par exemple 5% (ou 1%) et si elle est plus petite, alors là on va commencer à douter de l'hypothèse zéro, voire la rejeter. Une mesure répétée se doit d'être DANS la courbe du monde tel qu'il décrit, ou bien elle n'est pas bonne. Pas bonne ? Au contraire, comme elle est une expérience, c'est elle qui EST bonne, et c'est la description a priori du monde qui doit être rejetée. 

A noter que l'anormalité de la mesure par rapport à une description qui se trouve fausse se trouve mesurée dans le cadre de la fausseté, qui se trouve alors prouvée comme incohérente avec le réel et donc fausse... 

On notera qu'il y a dans le monde fréquentiste deux attitudes, celle du vénérable Fisher qui veut prouver rationnellement et celle du moderne Pearson qui veut lui décider. Les deux attitudes sont mixées dans les pratiques scientifiques courantes. Notons que Fisher adopte une attitude Popérienne: l'hypothèse nulle est la référence et reste une hypothèse réfutable. Quand quelque chose de bizarre se  produit, soit il s'agit d'un évènement rare possible et compatible avec la nullité de l'hypothèse, soit celle ci doit être remise en cause. C'est la fameuse "disjonction de Fisher" qui caractérise l'asymétrie Poperienne, critiquée par ailleurs.

Cette  histoire de p-value doit être comparée avec une autre histoire, qui est celle de l'intervalle de confiance, autre manière théoriquement équivalente de présenter les choses. L'intervalle est centré sur la moyenne du modèle, et a pour largeur 4 ou 6 fois l'écart type. Il faut que le test soit dedans pour que l'on puisse garder l'hypothèse nulle. 

La Gaussienne

Dans tous les cas, on se retrouve bien sur avec la répartition des observations possibles sur les abcisses d'une gaussienne... 

C'est la fameuse courbe en cloche, archétype de la courbe de densité de probabilité, limite continue des diagrammes en bâtons donnant chacun la probabilité d'un bloc de valeurs.  

Central Limite

De fait, le "théorème central limite" affirme que la somme de n lois gaussiennes d'écart type sigma donnera une loi gaussienne d'écart type sigma/racine(n). Plus n est grand, plus l'écart type final sera petit.

Le fameux théorème, merveille de la nature s'applique même si les lois des échantillons ne sont pas gaussiennes: dans ce cas, le résultat sera en cloche, mais avec un écart type non calculé ou à calculer... 

C'est ce qui justifie les sondages: si on prend un échantillon "assez" grand de taille N (la limite est 30), son écart type sera l'écart type de la "vraie" situation multiplié par racine(N). En fait c'est l'inverse c'est à dire que c'est l'écart type de l'échantillon qui divisé par racine(N) donne le "vrai" écart type... Celui ci est forcément petit: il "affine" les échantillons.

Mais bon, l'écart type sigma d'un échantillon permet ainsi de calculer de manière "sure" le vrai écart type... A partir de là l'intervalle de confiance de la moyenne de l'échantillon, qui elle est imprécise, sera de plusoumoins 2*sigma/racine(N) à 4 sigma et on peut y aller (programme de seconde).

On remarque que g(2*sigma, sigma) vaut 0,05 pour sigma valant 1, il suffit de regarder le dessin d'ailleurs. Mais en fait, le coup des 95% est en fait l'intégrale de la gaussienne entre -2*sigma et +2*sigma, qui vaut 0,95... On dira que la moyenne effective est donnée par la moyenne de l'échantillon "avec une confiance de 95%". 

Revenons au théorème central limite; sa formulation exacte est que la limite de la somme de tout ensemble de lois d'écarts types sigma dans un intervalle donné, divisé par sigma*racine(n) et centrées sur leurs moyennes sera l'intégrale de la gaussienne centrée réduite sur cet intervalle. La division par sigma permet de se ramener à la courbe archétype.

Plus exactement, la suite Zn avec Zn = RAC(n) *  (Xn - mu)/sigma  converge vers Z, gaussienne centrée réduite.

 

La Gaussienne centrée réduite

Rappelons que la fameuse courbe centrée sur zéro si elle a un paramètre sigma de 1, représente une distribution de probabilités dont l'écart type est sigma, a pour valeur maximale 0.4, est quasiment nulle en 3, et a pour valeur en 1 0.25. L'intégrale de la courbe est bien sur UN. 

  

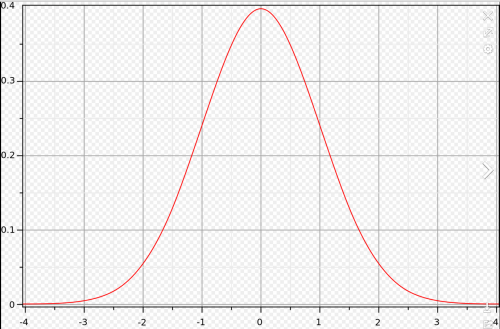
On notera l'utilisation de sigma, ici UN, le "3 sigma", opportunément transformé en "6 sigma" pour prendre toute la largeur de la courbe, et qui caractérise toutes les possibilités pour un objet d'être DANS l'hypothèse nulle. De fait, être hors du 6 sigma, c'est vraiment mal, ça ne devrait jamais se produire, et l'hypothèse nulle doit être rejetée... 

Linguistiquement, le 6 sigma est un critère de qualité, il permet, quand on VEUT imposer l'hypothèse nulle, de rejeter la mesure, comme non conforme au critère, quand on veut imposer soit la vérité absolue de l'hypothèse, soit une "politique" de qualité. L'objet fabriqué selon la mesure foireuse peut alors être poubellisé. 

On va alors considérer le 4 sigma. Et bien il se trouve, et cela reste à démontrer que l'on a là précisément le fameux intervalle de confiance à 95 % dont tout le monde parle !! En gros, l'intervalle de confiance c'est  plusmoins 2 sigma.

Pour le démontrer, fastoche. La loi gaussienne réduite ci dessus a pour équation

g(x,sigma) = exp(-x^2/2*sigma^2) / sigma*racine(2*PI)  avec sigma == 1

Courbe de densité de probabilité, dont l'intégrale dit "gaussienne" vaut 1 entre moins et plus l'infini. 

ll se trouve que cette intégrale n'a pas de formule simple, et n'est donnée que par des tables ! Par exemple le fameux 0,95 est incalculable à la main et ne vaut en fait non pas pour 2, mais pour 1,96.... La fonction PHI, répartition de la gaussienne de moins l'infini à x n'a pas d'expression analytique ! 

Un autre point est qu'on peut aussi jouer avec la forme initiale du théorème, qui partait d'une somme de "lois" (ou de "distributions") binomiales (les tirages à pile ou face avec une pièce truquée). Ces sommes de lois sont appellées aussi "de Bernouilli", le tirage principal ayant la probabilité "p", et on fait "N" tirages. La "loi" c'est la probabilité d'obtenir k fois la bonne face, avec k entre 0 et n. La loi c'est:

C(n, k) p^k (1-p)^(n-k))

Quand N tend vers l'infini, cette loi, dont l'écard type est racine(p*(1-p)*N), centrée sur sa moyenne N*p, et divisée par son écard type, et tend vers la gaussienne centrée réduite.

Un peu d'histoire

Laplace brilla avec cette histoire, en appliquant son raisonnement, tout issu des lumières, à la proportion de naissance de garçons dans la population qui se trouve supérieur à celui des filles, et cela partout en Europe, dans un rapport de 22 à 21. Or, en cinq ans, sur 2009 naissances à Carcelles le Grignon on observa la naissance de 1026 filles. Et bien cela est à l'intérieur de l'intervalle de confiance à 2 sigma ! Laplace exprime la chose en se ramenant au jeu de "croix" et "pile": la probabilité pour que cela arrive est inférieure à celle de tirer 4 fois "croix" de suite et donc non significative.

Les lois dérivées de la loi normale.

On a deux lois dérivées de la gaussienne, et qui servent dans les tests d'hypothèses. 

Student

D'abord quand le nombre d'éléments d'un échantillon test est inférieur à 30, on n'a pas la loi normale comme aggrégation des échantillons, mais la loi de Student à N degrés de libertés, N étant la taille de l'échantillon - 1, sachant que les probabilités ont pour somme 1. On fait comme avec la loi normale, à part qu'on regarde dans la table de Student pour contrôler la p value. 

kiki hideux

Et puis on a le Khi 2, X^2. Là c'est tout une poème car cela ne ressort pas du test d'hypothèses à proprement parler, mais d'un autre types de test, quoique la même méthodologie soit mise en oeuvre. 

Le test archétype est celui de l'indépendance de deux caractères. On part d'une distribution en n caractères (n plus petit que 10, ce sont les degrés de liberté) et on compare avec une distribution test.

L'idée est que sous l'hypothèse nulle, et qui est toujours que tout va bien, on va calculer "une statistique du khi 2", un nombre dont on va mesurer dans une table s'il a pour probabilité une valeur inférieure à un seuil d'acceptablité. Si oui, et bien on peut rejeter l'hypothèse nulle... 

Il faut bien comprendre que le khi deux n'est qu'une variante de la gaussienne, permettant de jauger les probabilités d'apparition -sous l'hypothèse nulle- d'une répartition particulière de valeurs dans des tableaux croisés. 

On se ramène donc à calculer un tableau croisé de référence, conforme à la distribution de l'hypothèse nulle, et on calcule alors une "statistique", le nombre:

     Sigma (1,n)   (xi_observé - xi_référence)^2 / nb xi 

Puis, on détermine le nombre de degrés de liberté, typiquement "n - 1". 

On consulte alors la table du khi deux.... 

On remarque ainsi que à 5%, la table donne pour les degrés de liberté 1,2,3 les valeurs 4,6,8

 

Le Sida encore

Reprenons en considérant la valeur-p pour le test du Sida. L'hypothèse nulle est de ne pas avoir le Sida, bien sur... Le test est positif, ce qui n'arrive que dans 1% des cas. C'est super faible n'est ce pas ? Et bien non ! Cela n'est pas du à la gaussienne, mais à la prévalence et au fait que la valeur-p ici de 1% (probabilité conditionnelle testpositif/passida) est abusivement décisionnelle si comparée à 5%.

La stratégie de la p valeur est donc prise en défaut, si on ne se méfie pas. Ce qui fait que certains recommandent toujours le seuil de 1% (4). Cela fut remarqué dans les années 2000 à la suite d'un grand nombre de p values trop minuscules (ou estimées telles) responsables de l'apparition trop non reproductible de phénomènes extraordinaires. 

On tremble en pensant au glyphosate... 

Le facteur bayésien est considéré supérieur, il s'agit de calculer H0/x : H1/x  , le rapport des vraisemblances. 

Pour ce qui concerne notre cas, on obtient oui/ok : (1 - oui/ok) = 10^(s-q).

Plus q est  grand, c'est à dire que la prévalence est faible, et bien on mesure l'insignifiance du test, c'est à dire son incapacité à contrer l'hypothèse nulle.

Avec q=4, et s=2, le facteur de Bayes est de 1% 

Au contraire, si la sensibilité suffisante, le facteur sera supérieur à UN, et donc le test "fort": on pourra alors avoir le sida, par exemple, si q=s, le facteur de Bayes sera de UN.

Le facteur de Bayes est un bien meilleur estimateur que la p-value ! 

  

(1) http://www.laeuferpaar.de/Papers/Sprenger_Bayes+Freq.pdf

(2) http://www.aly-abbara.com/utilitaires/statistiques/sensibilite_specificite_vpp_vpn.html#Q

(3) Pearson, Fisher et Bayes: http://udsmed.u-strasbg.fr/labiostat/IMG/pdf/testfreq.pdf

(4) https://royalsocietypublishing.org/doi/full/10.1098/rsos.140216

(5) le khi deux https://alea.fr.eu.org/git/doc_khi2.git/blob_plain/HEAD:/khi2.pdf

(6) la table du khi deux: http://www.math.univ-metz.fr/~bonneau/STAT0607/table_khi2_complete.pdf